The Star-Shaft Theory of the Great Pyramid – Busted
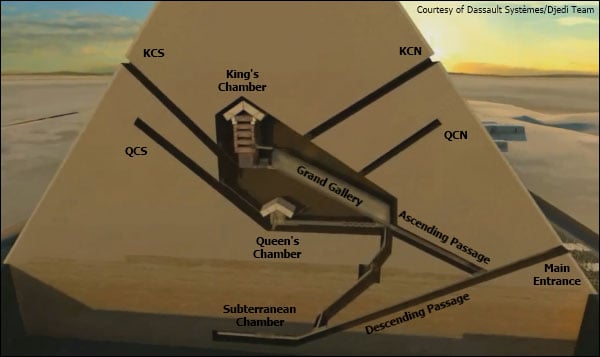
Many Moons ago a theory was proposed, which claimed that the small shafts inside the Great Pyramid pointed towards certain stars in the night sky. Furthermore, because the position of these stars changes with the changing millennia, due to the precession of the equinox (the slow precessional wobble of the Earth), a precise date for the construction of the Great Pyramid could be derived. The southern shafts were said to point towards Sirius and Al Nitak in the belt of Orion, while the northern shafts pointed seemingly randomly into the northern skies. The allocated stars in the northern skies were Kochab and Thuban, with the latter being claimed as being the pole star in 2450 BC.
But this is all rather disingenuous. None of these northern stars are significant in brightness, position or composition, and the claim that Thuban was the ‘pole star’ is not entirely correct. In reality, Thuban was displaced by 2° from the celestial pole in that era, and displaced a further 0.5 ˚ from the position that the shaft angle points at. *1 Despite the theory being artificially forced-to-fit in this manner, it has almost become established as a fact. Open any serious historical report or book on the pyramids, and readers will invariably see a picture of this shaft-pointing theory, and a therefore a date of 2450 BC for the Great Pyramid.

Fig 1. The star-shaft pointing theory. The southern shafts point at Al Nitak and Sirius, while the northern shafts point somewhat randomly towards the circumpolar stars.
Furthermore, because the Sphinx was designed as an image of Leo, it too can provide a precessional date for the construction of the Giza plateau. It does so by observing the constellation of Leo rising at dawn at the vernal (spring) equinox, which will only happen in certain eras. But while the date for the Great Pyramid derived from the star-shaft pointing theory was 2450 BC, the Giza date derived from the rising of Leo was 10,500 BC, which implies that the entire Giza plateau was very ancient indeed.
And so we can immediately see why Egyptologists have jumped upon the popular star-shaft bandwagon, rather than the lonely Leo bandwagon. The historical ‘experts’ date the construction of the Great Pyramid to about 2550 BC, but this date is based upon some highly disputed evidence for a poorly daubed cartouche of Pharaoh Khufu, situated way up in the attic-chambers above the King’s Chamber. But no pharaoh in his right mind would ever design a tomb that did not have its internal walls plastered and engraved with his great name; with images of the supportive and approving gods; and with texts and quotes from the Book of the Dead. Clearly, the Great Pyramid is not the tomb of a pharaoh. And no royal mummy has ever been discovered in an Egyptian pyramid. Conversely, just because a succession of English kings are buried in Westminster Abbey, does this mean that this great cathedral is merely a tomb? Think about it. The megalithic pyramids at Giza and Dahshur are most definitely not tombs.
Anyway, as readers can see, there is a huge disconnect between the astronomical dates derived for Giza. We appear to have the Giza plateau being designed in 10,500 BC, but some of the pyramids not being built for another 8,000 years. Clearly something is wrong with the theory here, and that something is the star-shaft pointing theory, which is wrong with a capital ‘W’. Or should that be: wrong with a capital ‘B’? And we know this bold assertion is true, because the small shafts inside the Great Pyramid have a completely different function. They were not designed to point at stars.
As with everything the great architect of Giza did on this site, the answer to the riddle of the small shafts is extremely simple, but nevertheless very clever and quite lateral. Rudolf Gantenbrink nearly solved this riddle when he commented on his web-site that the King’s northern shaft embodied the ratio of 7 : 11, as did the Great Pyramid itself. In recent updates to Rudolf’s Cheops web-site this snippet of information appears to have been deleted, which is a shame because it was probably the closest I have seen anyone get to solving the riddle of the shafts.
What Rudolf was implying is that the shaft angle of 32.5° in the King’s north shaft gave this shaft a specific set of dimensions, and so the linear dimensions of the shaft are connected to the ratio 7 : 11. If the King’s north shaft were to be resolved down into its simplest possible figures, the vertical rise of a triangle formed by this shaft would be 7 units, and the distance along the base would be 11 units – hence the 7 : 11 ratio mentioned by Rudolf. This was highlighted as being somehow special, because the pyramid itself also has a 7 : 11 ratio in its dimensions. If the pyramid’s height were reduced down to 7 units, then the base length would be 11 units – the ratio of 7 : 11 once more. So, it seemed that the architect was using this ratio as a guide in many of his calculations.
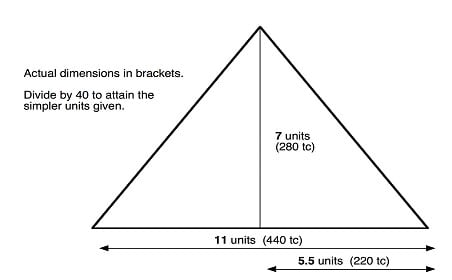
Fig 1.The fundamental dimensions of the Great Pyramid are 7 : 11.
Various writers have previously mentioned this 7 : 11 ratio for the exterior of the pyramid. In fact, it is even in Petrie’s Pyramids and Temples of Gizeh amongst many others. And the 7 : 11 ratio of the Great Pyramid’s external casing stones has occurred because the pyramid is constructed using the mathematical constant, Pi, as a model or guide. The simplest Pi ratio that maintains whole-number values on both sides of this mathematical constant is 7 : 22, and it was from this ratio that the 7 : 11 ratio for the pyramid’s external dimensions was drawn. The increase from 11 to 22 is due to the formula for a circle being multiplied by 2 (ie: 2 x Pi x r).
However, the complete solution to the small shaft riddle came when it was noticed that the numbers involved in the shaft angles, also embody these very same Pi ratios (both the angular elevation, and the linear dimensions of the shafts). The shafts themselves deviate up and down by a few tenths of a degree, but the average trajectory is quite reliable. If we assume that the architect was only constructing angles to the nearest 0.5°, the angles involved in the four small shafts that branch off from the Great Pyramid’s main chambers are 45°, 39.5°, 39.5° and 32.5°. *2
And if we plot those angles and lengths on a cross section of the pyramid, something interesting happens – the rise in each shaft is exactly 70 Royal or Thoth cubits (tc). And 70 tc is exactly 1/4 the 280 tc vertical height of the pyramid itself. So the linear dimensions of the small shafts, including their all-important vertical rise in cubit lengths, are mathematical and intimately related to the cubit dimensions of the pyramid itself.
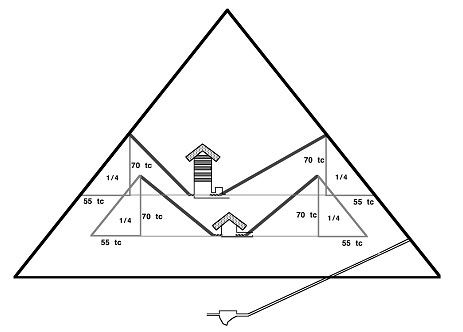
Fig 3. The vertical rise of the small shafts is 70 tc in each case, or 1/4 the 280 tc vertical height of the Great Pyramid.
And while this is all quite clever, there is more to this shaft symmetry, much more. If we subtract the larger angle from the smaller angle on each side of the pyramid (the north and south sides), the numerical differences between the angles are as follows:
45° minus 39.5° = 5.5°
39.5° minus 32.5° = 7°
The value of 5.5 is obviously 1/4 of 22.
Surprisingly, here are those same Pi ratio numbers yet again (7 : 11 or 7 : 22), but here they are involving angles, not lengths. Again, the complex nature of these shaft angles can be seen. They not only produce linear dimensions that are intimately related to the dimensions of the pyramid, but the numerical differences between their angles is also intimately related to the dimensions of the pyramid. This is a surprisingly complex thing to achieve, especially as the starting point for all these numbers is fixed by the mathematical constant, Pi ! This is achieved in part because the pivotal angle of 39.5° can be derived from (2 x Pi) 2 , and also from the arc-sine of 7/11 (or 1/2 Pi).
And the really important outcome of all this surprising mathematical symmetry, is that it totally destroys the star-shaft pointing theory. Readers can clearly see that the lengths and angles of the small shafts in the Great Pyramid use the mathematical constant Pi as their fundamental design criteria. They are Pi-based shafts. But this means that their angles of elevation are fixed by Pi, and not by the position of a particular star in a particular era. A Pi shaft angle cannot point at a particular star; it can only ever point at a fixed angle, and so any star-pointing can only be random. But if you are allowed the freedom of changing the era, which changes the angle of elevation of the star via precession, then of course you can make the star-pointing theory fit. If we discovered a shaft angle of 55°, this would equate to the position of Orion in about 4450 BC. And so we can continue, ad infinitum , for any angle and any era. The star-pointing theory is infinitely flexible, and therefore infinitely false.
Coordinates
So if these small shafts were not pointing at stars, then what were they doing? They were clearly important, as their complex design must have doubled the construction-time for the pyramid, as Rudolf Gantenbrink demonstrated with his detailed engineering designs for the pyramid. Please see http://www.cheops.org for Rudolf’s professional diagrams and detailed explanations for these small shafts. Surprisingly, the answer to the small-shaft conundrum lies in a mathematical challenge that comes straight out of high school. Let me explain.
The Pi ratio of 7 : 11 is all about lengths, not angles. The angular differences we have used, of 7° and 5.5°, are angular measurements and therefore have nothing to do with the linear measurements that are fundamental to the Pi ratio. So the architect has devised a riddle for us to solve – ‘When is an angle not an angle but a length?’ This may sound like an impossible question to resolve, but the answer lies on every map. To plot a position on a map we need a latitude and longitude. But when using this plotting technique, it is convenient to have a distance measurement system that is related to the dimensions of the Earth itself. Thus the unit used in nautical navigation is the Nautical mile, which is defined as being 1/21,600th of the circumference of the Earth, or 1/60th of a degree of latitude. As an aside, the length of the Nautical mile is therefore twice the Great Pyramid’s circumference.
So the answer to our architect’s crafty conundrum lies in the definition of the Nautical mile, for this unit is related to the size of the Earth and it can therefore be measured as an angular measurement, focused on the center of the Earth. One degree of arc at the center of the Earth equals 60 Nautical miles of latitude on the surface of the Earth; and so we have found a very neat and logical occasion when a linear length is defined in terms of angular measurement. It happens every time a navigator plots a position on a map. So it would seem that our shaft angles are actually coordinates on a map.
What every grand quest needs is an ancient map, with ‘X’ marks the spot inscribed upon it. Strange as it may seem, it appears that we have exactly that within the Great Pyramid. As is explained in K2, Quest of the Gods , the outline of the Great Pyramid’s chambers represents a perfect outline of the continents of the Earth. But of what use is a map of the world, without some coordinates to place upon it? An interesting map requires an ‘X’ marks the spot marked on it. Well, we now appear to have just that – a set of coordinates to place upon our Great Pyramid map!
Understanding this clever conundrum allows us to plot the Great Pyramid treasure-map, at long last. We have four shaft angles that can be used for this exercise, and therefore four coordinates that can be plotted on a map. These angles are:
King’s Chamber 45° & 32.5°
Queen’s Chamber 39.5° & 39.5°
And in doing so, something quite remarkable happens. Because the differences between these shaft angles were exactly 7 and 5.5 degrees, as was explained previously, the two points on the world-map are in very specific locations relative to one another. And if the points are joined up, as has been done in the following diagram, the triangle so formed measures precisely 7 x 5.5 degrees of latitude and longitude respectively. If the triangle is doubled up with its obvious symmetric partner, then the resulting triangle drawn on the surface of the Earth becomes 7 x 11 degrees in size – which is exactly the same dimension ratio that was employed in the Great Pyramid itself.
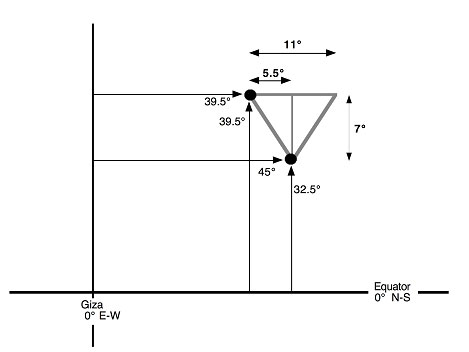
Fig 4. Plotting the Great Pyramid’s shaft angles on a map, gives a triangle with the same ratios as the Great Pyramid itself.
Here, drawn on the surface of the Earth, is an immense triangle that has exactly the same ratio of dimensions as the Great Pyramid, and this has been drawn using the angles given to us by the shafts inside the Great Pyramid itself. Is this a coincidence? I think not.
Karakoram triangle
The next question we have to ask is, where on the surface of the Earth does this large pyramidal triangle lie? As is explained in K2, Quest of the Gods , if we use Giza as our longitudinal zero meridian, then the great triangle lies across the western Himalaya, in a region known as the Karakoram. And so a large expedition was mounted many years ago, to take a look at this location up into the high Himalaya. And since there are no roads in the region, the long trek to the center of this large triangle took nearly three weeks of hard hiking across the almost impassable terrain.

Fig 5.The high trail into the Karakoram. These are the almost impassible paths that lead to the very center of the large triangle that was discovered in fig 4.
And what was the result of this long expedition? The surprising answer is that high up in the Himalaya there is an almost exact copy of the Great Pyramid. Yes, seriously! In the very center of this Karakoram triangle there is a large mountain that is pure white, just as the Great Pyramid used to be before its Islamic guardians pilfered the cladding stones. More importantly, this is a square-based pyramid-mountain, orientated to the cardinal points, and it has a glacier extending from its base at the same 14° angle as the causeway that extends from the Great Pyramid.
Pictures and a precisely contoured map of this pyramid-mountain are to be found in K2, Quest of the Gods , and so readers can see for themselves that there is indeed a large copy of the Great Pyramid way up in the Himalaya. Thus the pyramids of Giza are not simply representations of the stars of Orion, they are also representation of mountains. The tallest pyramid at Giza is all white (all snow covered); the Second Pyramid has a thin layer of granite at the base (a snow-line on the mountain, with a few exposed rocks at the base); while the Third Pyramid has 1/3 of its surface composed of granite (a much higher snow-line, with many rocks exposed at the base). And do bear in mind the sequence of this amazing discovery:
i. Firstly, the outline of the continents was noticed in the layout of the chambers.
ii. Then the function of the shafts as cartographical coordinates was realised.
iii. Then these were plotted and a location discovered.
iv. Then a detailed map was ordered from China, which took four weeks to arrive.
v. And only then was it noticed that there is a copy of the Great Pyramid up in the high Himalaya.
This is a remarkable sequence, is it not?
The detailed map of this Himalayan pyramid-mountain is reproduced in K2, Quest of the Gods , but here is a satellite photo of the region. The pyramid-mountain is in the upper center of this image. Can readers see it? Be advised that this image is orientated slightly east of north, so the pyramid-mountain will be skewed anti-clockwise slightly. In reality, it is orientated very precisely with the cardinal points.
So how do readers imagine this was achieved? How is it possible to discover a copy of the Great Pyramid up in the Himalaya? I feel, this intriguing quest has only just begun…..

Fig 6. A satellite image of the pyramid-mountain in the Karakoram. It is located in the upper center of this image, with a puff of cloud on it summit.
Related Post
A shocking documentary proves that mermaids do exist
SHOCKING Revelation: Thuya, Mother of Queen Tiye, Was the Grandmother of Akhenaten and Tutankhamun—What Ancient Egyptian Secrets Did She Leave Behind?
Breaking News: Astonishing Discoveries at Karahan Tepe Confirm an Extraterrestrial Civilization is Hiding on Earth, and NO ONE Knows!
Breaking News: Researchers FINALLY Discover U.S. Navy Flight 19 After 75 Years Lost in the Bermuda Triangle!
NASA’s Secret Investigation: Uncovering the Astonishing Mystery of the UFO Crash on the Mountain!
Explosive UFO Docs LEAKED: Startling Proof That Aliens Ruled Ancient Egypt!
